The success of commercial music often depends on the use of effects, allowing the listener a new audio experience. Michael Jackson's album 'Thriller', one of the best selling albums of all time, used a drum machine which was a new concept at the time, and provided a dramatic foundation to the tracks. The drum machine stored the sounds in an 8 bit nonlinear format that provided a 12 bit dynamic range and a 5 bit active signal to noise ratio! The quality seems perfectly OK when listening to the album, and the effect of perfectly timed drums is stunning, but in today's terms the quality would be deemed completely unacceptable. The point is that the effect is often more important than the quality of the sound. In some cases, the effect is a degradation in sound quality. Effect design is a creative process, tapping the imagination of the developer, and is a completely open art.
Delay effects
The first popularized use of flanging was highlighted in the song 'Itchycoo Park' by Small Faces, recorded 40 years ago. Flanging is one of the fun things that can be done with a pair of analog tape recorders, which today may be difficult to find. In the days of analog tape, two recorders were set up with identical tapes, the outputs mixed together, and played at the same time. If one recorder was slowed slightly, so that the two would be slightly out of synchronization, a remarkable effect would emerge. As the opposite recorder is slowed, the two machines would cross through synchronization again, and when the sound passed through synchronization, the effect would seem to go 'over the top', an ecstatic, even orgasmic audio experience. The term flanging comes from the method of slowing a given machine, by lightly touching the flange of the source reel of a recorder to slow it down a bit.
When an audio signal is mixed with a delayed version of the same signal, the frequency response of the mixture takes on a very interesting shape. Such an arrangement is called a 'comb filter', on account of the frequency response shape:
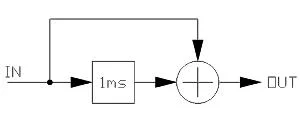
The plot is from 0 to 20KHz, on a linear scale. We can imagine that two sine waves, one shifted in time from the other will reinforce or cancel, depending on the frequency and the delay. In the case of the 1mS delay shown above, a 1KHz signal will be exactly in phase with the same signal delayed by 1ms. 500hz though, will be shifted by the delay by exactly 1/2 cycle, and the delay input and output will cancel when mixed together. The plot shows peaks at 0Hz, 1KHz, 2KHz and so forth, and dips at 500Hz, 1.5Khz, 2.5KHz and so on. When music is played through such a filter, and the delay is varied, the peaks and dips of the frequency response move throughout the audio spectrum creating the 'flanging' sound. Notice that if the phase of one of the signals is inverted (multiply by -1.0) at the mixer, the exact inverse of the frequency response is obtained, peak frequencies being converted to dips, and vice-versa.
This flanging effect can be psycho acoustically explained. Our ears are roughly 6" apart, and since the speed of sound is roughly 1000 feet per second, a sound to the right side of our head will arrive at the right ear about 0.5mS prior to arriving at the left ear. Our brains can determine the location of a sound source based on this delay time. In fact, signals are traditionally panned in stereo space by the adjustment of the relative sound level in the two stereo channels, but if a mono signal is fed directly to one stereo channel, and through a 0.5mS delay to the other, the level will be the same in both channels, but the listener (with headphones) will clearly identify the sound as coming from the 'early' side. This psycho acoustic panning can be used as an interesting effect. Flanging, with a continuously varying relationship between the early and late sounds, gives the effect of one's head slowly turning in space, as though the listener was floating and turning before the sound source. Interestingly, this is also the case even when the flanged sound is auditioned in mono.
Flanging programs usually sound best when the delay modulation is linear with time, that is, the delay changes by some constant fraction of a sample on every sample cycle. Often this is accomplished by setting up a software Low Frequency Oscillator (LFO) to produce a triangle waveform, with the peak of the waveform representing zero delay (over-the-top). Further, some feedback can be applied around the entire flange process to accentuate the effect. All variations on the theme are fair game: negative summation, as well as negative feedback around the flange block, even a higher frequency sine wave added to the LFO ramp!
In a DSP system with a sample rate (Fs) of 40KHz, 40 memory locations would be required to provide a 1mS delay.
As a note, when listening to a CD, the 44.1KHz sample stream is of course smoothed into a continuous waveform by the DAC in the system, but if one were to imagine the time period between samples and the speed of sound, the physical space between samples as the sound emerges from a speaker would be a little more than 1/4 of an inch per sample.
The Hass effect
When listening to two identical sounds mixed together, one delayed from the other, the sound quality is affected as a tone when the delay is short, and two distinct sounds if the delay is long. The delay time that lies between these two extremes is about 30mS, and the overall idea is called the Hass effect. Flanging is usually accomplished with rather short delays, causing the lowest primary notches to be around 100Hz (5mS delay). Longer delays verge on the impression of two sound sources, so the effect of chorus and vocal doubling both require delays at or around the magic 30mS range.
Chorus and Vocal doubling
The simplest method of 'fattening' an instrument or voice in the studio is to add extra tracks of a similar performance, as though an entire ensemble of musicians were performing at once. In actual performance, this may be impossible, so the effect of chorus can be used instead. Chorus is usually a delay, or multiple delays, all on the order of 20mS to 50mS long, slowly modulated by LFOs to produce slight variations in both pitch and time throughout the performance. Too fast a delay modulation can lead to vibrato effects, a subject which can be jumped to from here.
Vocal doubling, also referred to as slap-back echo, refers to a short delay that is used to fatten a voice, usually without much or even any delay modulation. Vocal doubling delays can be in the 30ms to 60mS range.
Phase shifting
The effect of frequency response notches moving in time, produces the head-turning-in-space effect, but may not need a true variable delay to be accomplished. The effect of phasing can be created by producing a few notches in the audio spectrum, and modulating their frequency slowly with time, to produce a similar effect. In analog electronics, this is done with a bank of all-pass filters, circuit elements that have a flat frequency response, but create a frequency dependent phase shift. The output of the filter bank is summed with the input, and at those frequencies where the filter bank output is out of phase with the input, a notch is created.
The all pass filter operation is complicated to explain, but the analog and digital versions are shown here:
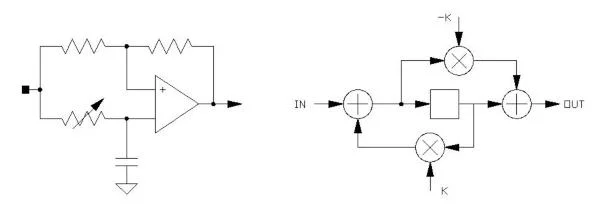
In both cases, the output is in phase with the input at low frequencies, but out of phase at high frequencies. Varying the resistor value in the analog version, or the K value in the digital one, will adjust the frequency where the phase is at the midpoint, 90 degrees. This filter is useful in not only making phase shift effects, but others as well. In the case of the digital variant, the delay is a single memory location (a register), but we will see later in the section on reverb where the digital all pass filter can make use of a longer internal delay.
Notice that the phase shifting effect produces only a few, lower frequency notches, whereas the flanger, using a real variable delay, produces notches out to the highest frequencies. Psycho acoustically, the lower frequency notches are responsible for the majority of the effect. In fact, when building digital flangers, you may wish to use a filter to slightly roll off the upper frequencies from the variable delay signal; the large number of notches at the highest frequencies can often become a 'distraction' to the intended effect.
A Note on the FV-1 Delay memory addressing
In a general purpose processor, memory is accessible as a block with fixed addresses. If you wish to implement a delay, you must write to a new location on every sample cycle, then read from a different location that is also changing on every sample cycle, ultimately reading the originally written data some number of sample cycles later. On each memory access, you must somehow calculate the memory address for each operation, for both reading and writing. The FV-1 is designed to do this for you, automatically. All accesses to the delay memory (but not the register bank) are to addresses that are automatically generated from a relative address that you specify in your program, plus a memory offset counter that decrements at the start of each new sample cycle. As a result you can write programs that initially define the areas of memory you wish to use for delays, and in your written instructions you can refer to the start, end, or any point between the start and end of a delay when reading signal outputs. Writing is usually to the start of the delay, the base address.
When using this scheme, you must be aware of it, but you can largely ignore concerns for all of that which is going on in the background.
Continuously varying delays
When we attempt to change a delay in a DSP program, we can hardly jump from one delay length to another, as this would cause abrupt changes in the sound. Normally, we would establish an area in memory for the maximum delay, and change the delay length by adjusting the read point from memory. When smoothly varying a delay, the specific delay point we calculate will often lie between two delay samples. The easiest way to obtain such a fractional delay output result is through linear interpolation between the two adjacent samples. We read each of the two samples and multiply each by it own interpolation coefficient, then sum these two products to obtain a valid mid-sample result. The interpolation coefficients must both sum to unity. In practice, a virtual address is calculated in the DSP code, which is then used to access a read point form memory.
An example:
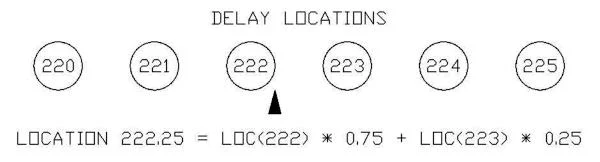
Notice that the closer the virtual sample is to a real one, the higher the interpolation coefficient. Confusing the proper interpolation coefficients is a common mistake in writing DSP programs.
Vibrato
Vibrato is technically a repetitive variation in pitch at a frequency that usually lies in the range of 2 to 6 Hz, and is different from tremolo. This is accomplished by a short variable delay, the delay time being modulated by a sine wave. As the delay shortens, the pitch of the output will raise, and as the delay lengthens, the pitch will fall. Attempting to obtain a constant pitch change from this technique will quickly lead to running out of memory, but if the delay is modulated with a sine wave, vibrato can be accomplished with a small delay. The pitch change is the result of the rate of change of delay. If you code a vibrato using say, a 2mS delay, and modulate it over its entire range with a sine wave LFO, the pitch change will be three times as great at 6 Hz than it will at 2 Hz.
The extremes of the pitch change can be calculated, using some simple logic: The LFO will be producing a sine wave that in the above case will modulate a 1mS delay by a +1mS and a -1mS amount, leading to a delay that spans 0 to 2mS. Sine waves have the property that at their greatest rate of change is while crossing zero, and at this point, the rate of change is 2*π *F*peak amplitude. At an LFO frequency of say, 4Hz, the sine wave will be changing at 2 * π * F * the peak delay variation, or approximately 2*3.1415*4*1mS=25.13mS/second. This is to say that the pitch will be changed by about 0.02513 of it's original value. In music, one semitone represents a frequency increment of about 0.059 (roughly 6%). This 4Hz, +/-1mS vibrato would produce a peak pitch variation of about 1/2 a semitone, which may sound extreme in some cases, but then, not enough in others.
Chorus effects will also demonstrate a vibrato effect, as any changing delay will affect pitch. This is often the limiting factor in the chorus effect, as too great a delay sweep will lead to extreme off-notes. Then again, this may be the objective.
Pitch transposition
Pitch transposition is a change in pitch that corresponds to music; that is, it is a change by a factor, not an increment. To illustrate, an octave is a factor of two in frequency. If you were to pitch transpose a 1KHz tone up an octave, it would become 2KHz, and if brought up another octave, 4KHz. Transposition of music allows the pitches to remain in musical harmony, simply set into a different key.
To perform pitch transposition, we will need to use variable delays, but as we already know, we cannot change a delay, increasing or decreasing its length for very long, or we will eventually run out of memory. To retain the basic character of the music while changing its pitch through a variable delay technique, we will need to occasionally change our moving delay read pointer as it approaches one end of the delay to the opposite end of the delay, and continue on. This abrupt jump in the read pointer's position will be to a very different part of the music program, and will certainly cause an abrupt sound. The problem can be largely overcome by establishing two delays, let's name them A and B, both with moving read pointers, but with their pointers positioned such that when the read pointer of delay A is just about to run out of 'room', delay B's pointer is comfortably in the middle of it's delay's range. We then cause a crossfade, from obtaining our transposer output from delay A to the signal coming from delay B. When the delay B pointer begins to run out of space, (just prior to pointer repositioning), we crossfade back to delay A. The delays can in fact be a single delay, with two read pointers properly positioned.
The rate at which we crossfade, the delay lengths we use, and the amount of pitch transposition we require will determine the resulting naturalness or unnaturalness of the transposed result. In many cases, especially for complex music, the effect is quite believable.
Barber pole flange
A fractional pitch transpose, a detuning of only perhaps a tenth of a percent, when added with the input, can cause an effect called 'barber pole flanging'. Like the rotating red and white spiral that would be outside barbershops as an advertisement, This flanging sound seems to always be sweeping up or down, continuously. It is a very interesting and useful effect. For best results, this is done with a very short delay, and the signal to which the result is added should be delayed a bit too. Experimentation is necessary.
Pitch shifting
Pitch shifting is different from transposition. While transposition is a change in pitch by a factor, pitch shifting is by an increment. The two terms are often confused, and used interchangeably to describe the more common and useful pitch transposition. If we pitch shift by 1KHz, then 1KHz becomes 2KHz, and 2KHz becomes 3KHz; not a pleasant musical transformation! Pitch shifters are used to disguise voices and create non-harmonic effects, and when used in conjunction with transposers can allow a talk show host to have hilarious conversations with himself (as with Phil Hendrie (sorry Phil)).
The pitch shifting process makes use of the interesting mathematical properties of sine waves, and their 90 degree phase shifted brothers, cosine waves. The process effectively multiplies an LFO by the input signal, but must do so using complex math. By complex is meant not just difficult and complicated, but instead, the use of SIN and COS LFO signals, and the use of both the input signal and a copy of the input that is shifted 90 degrees in phase.
Obtaining an input signal copy that is phase shifted by 90 degrees would be easy if just a single input frequency was involved, as we have already seen the rather simple all-pass filter that will perform this function. To produce a constant 90 degree phase shift over a wide frequency band however, is a bit more difficult.
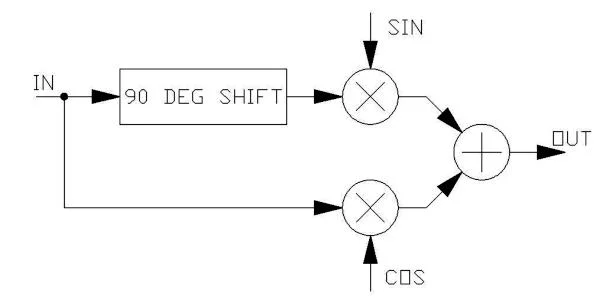
The terms SIN and COS are from an LFO that produces these two signals, and the amount of pitch shift will be the frequency of the LFO, in Hz. The input phase shifter is actually two banks of all pass filters that are designed to produce a continuously varying phase with frequency, and the difference between their outputs is approximately 90 degrees over a wide frequency band. In practice, the input to the COS multiply is from one phase shifter, the input to the SIN multiply is from the other. Take note that any input DC value (input offset) will be also shifted, causing the LFO frequency to be found at the output! The pitch shifter will pitch shift either up or down, based on the phase relationship between SIN and COS; normally, SIN lags COS by 90 degrees, but if your LFO can be driven to produce a negative frequency (as in the FV-1), then COS will lag SIN. Pitching up and down then becomes a matter of the LFO producing a positive or negative frequency. Wild notions, no?
Designing the all pass filter banks for the pitch shifter is difficult; a task made easier by limiting the signal frequency range to only that which is required. For voice, perhaps 100Hz to 6KHz will do.
Tremolo
Where vibrato is the sinusoidal variation in pitch, tremolo is the sinusoidal variation in amplitude. This is easily accomplished by simply multiplying the input signal times an LFO sine wave that varies from 0 to 1 (instead of -1 to +1). Because the average signal level will result in being half of the original, you may consider multiplying the input by a 0 to 2.0 sine wave, or simply adding gain to the algorithm.
Ring modulation
This is simply tremolo at a higher rate, and with the LFO swinging both + and -. An ugly sound, which might be exactly what you're looking for. This is perhaps the the most repulsive of the ugly sounds, so if that's you're interest, it is the most beautiful of the ugly sounds.
Simple filters
Filters can come in all shapes sizes, types and styles, simple or highly convoluted, easy to come up with coefficients for, or agonizingly difficult. The subject is huge, and applications are vast. The simplest filter is the single pole low pass:
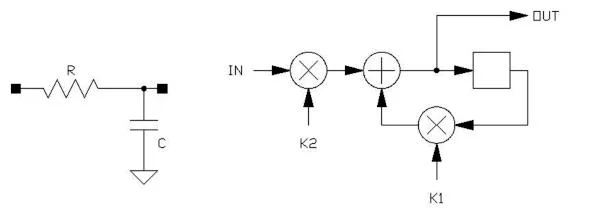
The cutoff frequency is determined by K1 and K2, the sum of which must be equal to 1 for the filter to have unity gain. For a given sample period t and a desired -3dB cutoff frequency of F, the value for K1 is equal to e-(2πFt) . This illustration shows the filter being accomplished with two multiplies, but since K1+K2=1.0, it can be done with one multiply thusly:
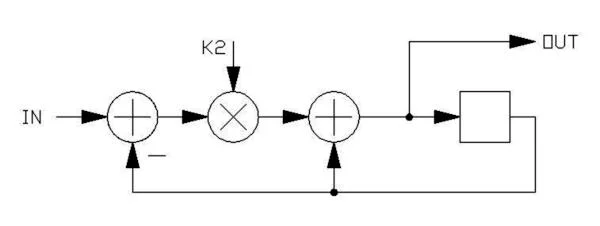
The single controlling coefficient, K2, adjusts the -3dB point, and is equal to 1-K1 in the previous equation.
A high pass filter can be constructed from the low pass, by simply subtracting the output from the input of the low pass design, and shelving can be provided by an adjustable coefficient. The shelf coefficient Ks should be negative to perform the subtraction, and would be set to -1.0 for the shelf to be infinite.
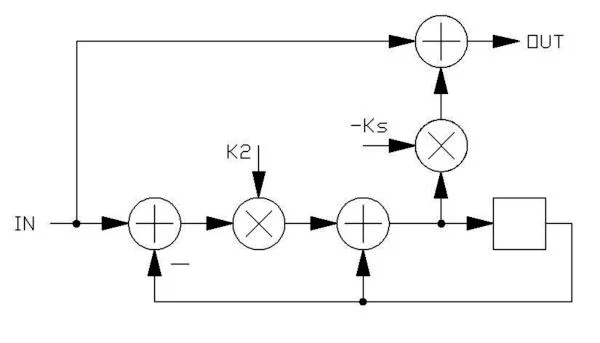
Because they are so useful, especially in reverb algorithms, special instructions in the FV-1 can perform this shelving high pass filter in two successive instructions.
The shelving low pass can be a derivative of the high pass with an infinite shelf:
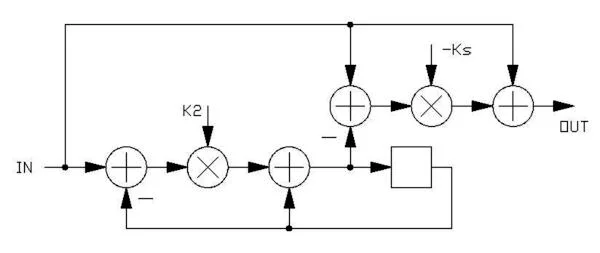
The FV-1 can also produce this structure in two successive instruction cycles.
One characteristic of the single pole filters is that the cutoff frequency is linearly dependent on the coefficients when used at the lower operation frequencies. Therefore, although the single pole characteristic is not dramatic as an effect, the frequency can be swept with simple mathematical functions from control signals such as a potentiometer position or a detected signal level. For the lower, more musical frequencies, K2 is roughly equal to (2πF)/Fs, where F is the cut off point, and Fs is the sample frequency.
Audio effects DSP applications are distinctly different from precision instrumentation DSP systems. The former only requires the desired resulting sound, which in most cases has no need for precision and leads to simple hardware; the latter however, may require high accuracy and precisely derived coefficients. Music is to one's taste, which is imprecise by nature! Programming an effects DSP is more of an art, programming a scientific instrument is solidly in the realm of mathematics. This gives the effects programmer a significant degree of freedom in choosing DSP structures that may not be perfect, but accomplish the task quickly and with easily derived coefficient values.
Peaking filters
Bandpass filters and peaking low pass or high pass filters require a 2-pole design, which is considerably more complicated. There are several approaches, but the most straightforward is the biquad filter. This filter uses two integrators in a loop, and can produce high-pass, low-pass, band-pass and notch outputs, depending on how signals are input, and how outputs are taken. An integrator is simply a register and an adder, connected so that the register contains the continuous summation of input samples. Two integrators in a loop (with a sign inversion of the signal at one point) will form an oscillator, the frequency depending on the coupling coefficients. An oscillator is simply a peaking (bandpass) filter with infinite Q and a stimulated starting condition:
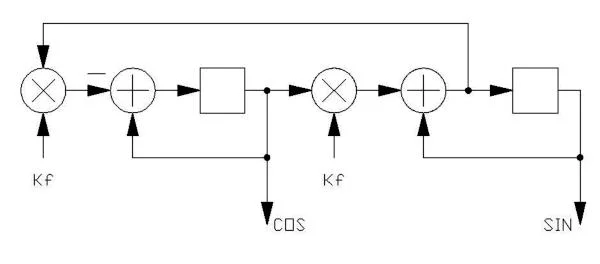
This is the structure of the SIN/COS LFO element in the FV-1, and when coded into a program can be the starting point for musical peaking filters. Signals could be introduced anywhere within the filter, but since an infinite Q filter will have infinite gain, it is of little practical use (although you may find that application!). The Kf value is used twice, and would be calculated (for low frequencies) much the same as K2 in the earlier, single pole filters. To become a more useful filter, the Q must be lowered (by introducing losses), and signals must be input and output. Filters of this type are very useful at lower frequencies, but are limited to peaking frequencies below about Fs/4. For most music applications, sweeping through the fundamental and lower harmonics of a signal, this is entirely adequate.
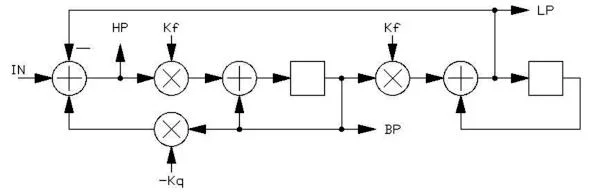
With a Kq value of perhaps -1.0, this filter is also a great way to split a signal into high and low frequency bands, each with 12dB per octave slopes. Diminishing the value of Kq will increase the filter's Q. In a sense, we may better consider Kq to be a damping coefficient. The filter produces a high pass output (HP) that is symmetrical with the low pass output (LP), and a band pass peak as well (BP). A notch can be created by adding HP and LP together. This is a remarkably flexible filter and easy to code. The above structure is particularly useful as a swept filter, as the filter's frequency is controlled entirely by Kf, in a linear fashion. The Q of this filter will remain reasonably constant over a wide range of Kf values.
If peaking (or cutoff) frequencies higher than about Fs/4 are required, they will be difficult to do without oversampling the filter. Oversampling simply means that the algorithm is written twice within the program, so to have the effect of being executed twice as often on the data samples. This technique allows the above filter to be swept over the entire DC to Fs/2 bandwidth.
In the case of fixed filters, ones that are not meant to be swept, a different architecture can be used, but as the coefficients are interdependent, changes to the coefficients cannot be done casually. The advantage of fixed filters is that they can reach to Fs/2 without the use of oversampling techniques. An example of one basic structure:
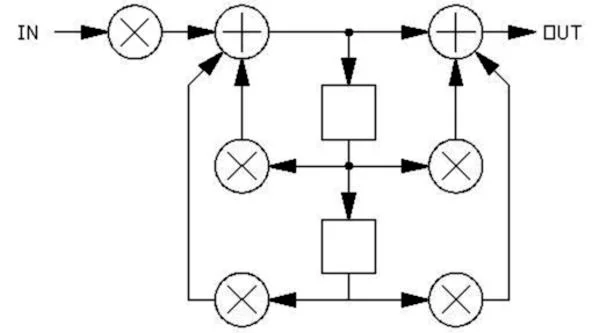
This filter form requires coefficients that must be calculated from an analog filter that has the required response, and such coefficients cannot be experimentally derived or modified with ease.
Reverberation
Echo can be easily achieved with a long, recirculating delay:
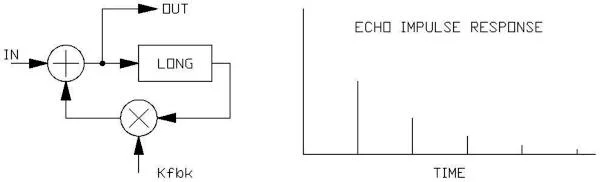
This is the typical 'karaoke sound' that was popularized in the 70's due to the development of analog delays using charge-coupled IC techniques. The tradition continues with karaoke today, despite the availability of the more desirable digital reverberation. The echo effect is in fact just a low reverberation density approach, but can still be characterized in terms of reverb time by measuring the time for a recycled impulse to fall by 60dB.
A more realistic abstraction of a natural reverberant space is produced by more complicated processing structures. The primary difference between echo and reverberation is a dramatic increase in reverb density, both initially, and with time as the reverb 'tails out'. This increase in density is provided by the all-pass filter, similar to the one used in phasing, but with a multi sample delay used in place of a single register. The all pass filter uses identical coefficients, but of opposite sign. The signs of the coefficients can be swapped (for reverb applications), causing a similar sound, but a different impulse response:
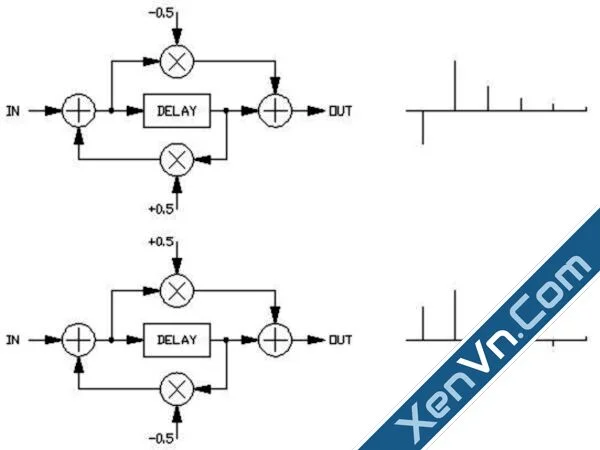
The important characteristic of the allpass filter, when built around a sizable delay is that although the impulse response is made more complicated, which is desirable in a reverb system, the frequency response, measured over a period of time, is flat. Recalling from the earlier discussion about delays, the summation of a delay with it's input causes a comb filter response, which far from flat. The FV-1 has the ability to perform the mathematics of an allpass filter stage (with fixed coefficients) in two successive processor operations.
When multiple delays and all pass filters are placed into a loop, sound injected into the loop will recirculate, and the density of any impulse will increase as the signal passes successively through the allpass filters. The result, after a short period of time, will be a wash of sound, completely diffused as a natural reverb tail. The reverb can usually have a mono input (as from a single source), but benefits from a stereo output which gives the listener a more full, surrounding reverberant image. A simple reverb loop:
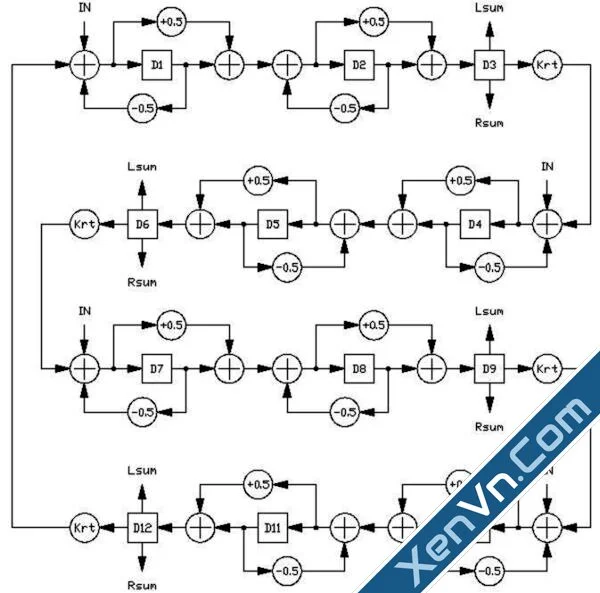
The terms Lsum and Rsum are taps from the delays, meant to be added (not shown) in different proportions to produce a stereo-like output. The coefficients are shown within the circles for simplicity. The term Krt controls reverb time. Shelving high pass and low pass filters may be added to the loop to control the decay of high and low frequencies, which produces a more natural reverberation, but are not shown. This loop is composed of four blocks of 2 allpass filters and a delay, although any of the blocks could contain 1 or 3 or more allpass filters, and the loop could be 2 or 3 blocks instead. There may be only one Rsum or Lsum per delay, and the input may be inserted at only 2, or even 1 spot within the loop. Stereo may be input by inserting the left input to one point in the loop, and the right input to another. Further, it is often useful to add a few series allpass filters in the input signal path, so that the signal inserted into the loop has a higher initial density. The construction of a reverberator architecture and the choices of filters, delays and output taps is very much an experimental art; there is no 'best' algorithm, just as there are no 'best' rooms, halls, or plates in the physical world.
Reverberators can be built that sound wonderful with drums; explosive, smooth and rich in a wash of density, and when coded in the FV-1, can be accomplished with as few as 20 instructions. When auditioned with a single sound however, they may have a 'ringing' tail sound, at the very end of the reverberation time. Many commercial tracks are cut with such ambience, but inexperienced engineers will be concerned about the ringing tail sound. In fact, this is entirely covered up by the active music in actual use. To remove the ringing sound, it is helpful to slowly modulate some of the delay lengths within the reverb loop, so that the output pattern is not fixed, but slowly varying, which smoothes out repetitive mechanical effects. This can be accomplished by a single SIN/COS LFO generator, modulating the lengths of one or two of the internal delays (delays or all-pass delays), using say, the SIN output in one place and COS in another.
The initial sound of a reverberator can be an important part of its overall quality, and is often achieved by the use of a tapped delay:
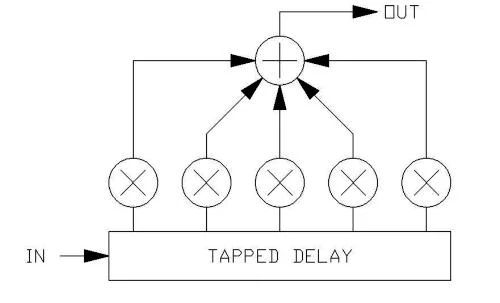
There can be any number of taps, each weighted by a multiply coefficient that exponentially decays with delay time. These initial reflections give a sense of dimension to the reverberator. The left and right outputs can be from different taps, giving a sense of direction to the 'room'. The left and right taps are summed with the taps from the reverberator which produces the reverb 'tail'.
Considerations when building a reverb
Do not expect a given reverb structure, with delays and coefficients well chosen, to sound good at extremes of reverb time. To build a good reverb is one thing, to build one that responds well over a wide range of decay times is extremely difficult; impossible, if not extremely complicated in design.
The total delay (excluding allpass filter delays) in the loop should be at least 200ms. Shorter delay time will lead to flutter, a repeating quality in the tail. The human ear is very sensitive to flutter in the 4 to 8 Hz range; very short delays will cause a tinny sound, moderately short delays will cause a noticeable flutter. If the flutter frequency is low, on the order of 1 to 2 Hz, the ear perceives the sound as 'evolving', not fluttering.
Placing variable delays in the allpass filters, even just in one spot or another, can help smooth out a reverb, giving the slight impression of motion, and suppressing a hardness, ringing or flutter problem.
The swapping of coefficient sign in some of the allpass filters can occasionally improve the overall quality.
Allpass filters with a coefficient of 0.5 will cause the reverberator output to 'build', leaving the listener with the impression that there is a delay in the reverb output; this can be improved with some early reflections from a tapped delay. Allpass coefficients on the order of 0.6 will build quicker, but be 'fat' during the initial sound period. Coefficients of 0.7 and above will sound more immediate, but can have the tendency to produce a 'ringing' sound.
Feeding the input into each block of the loop, and taking outputs, both left and right from each delay will lead to a very dense reverb, but because of the comb filter effects that are then produced, the reverb will not have a flat frequency response characteristic. Complete flatness of response is not really required, but sharp and narrow peaks of high amplitude cause the reverb to 'ring'. Consider taking fewer taps as outputs and inject the signal less often to get a flatter response.
Gated reverb and dynamic effects
Any signal can be detected and filtered, and in doing so, turned into a control parameter. In the case of reverb, the input signal can be detected and used to control reverb time. While the signal is active, above a certain threshold, the reverb time could be long or short, and then smoothly (important!) transform to the opposite extreme when the signal goes away. This can produce a powerful effect on drums, where the reverb is huge for a brief time, and then rather suddenly extinguishes some short time after the signal has gone. Likewise, a singer's voice can be surrounded with a fairly short reverb time while singing, which may lead to greater clarity, but then extend to a longer time between phrases.
Dynamic effects can take on any number of dimensions; truly an art form of high complexity. Peaking filters that track a signal's level ('autowah' effects) are a classic, but not a limiting example. LFOs that drive phasers, flangers, vibrato or pitch effects can be modulated in both value, amplitude, rate or intensity, depending on the effect and the desired results.
Signal detection is performed by several means: We could convert the normally +/- swing of the signal into + only, and then average the result with a low pass filter (average detection). We could alternatively use the more musically relevant RMS (root-mean-square) detection, which gives a result that is more closely related to apparent loudness; RMS detection requires that the signal be squared (multiplied by itself), which produces a positive output value, then averaged by a low pass filter, and finally square-rooted by the use of LOG and EXP functions, as the square root of (X)=EXP(LOG(X)/2). Finally, we could peak detect the signal into a filter, where any signal peaks that exceed the filter's value are loaded into the filter register. All of these techniques can find their way into controlling effect parameters.
When controlling the frequency of a filter, be aware that the musical scale is exponential, not linear. For example, if a filter frequency is to be controlled by a potentiometer, perhaps over the four octave range of 100 to 1600 Hz, the center of the pot would best represent 400 Hz, not 800Hz. The FV-1 contains both LOG and EXP functions so that such musically relevant conversions can be performed easily.
Compression and expansion
The control of program dynamics can be an important part of any effects toolkit. In the analog world, a VCA (voltage controlled amplifier) is often used to control gain, and in the case of a compressor (or limiter), the output of the VCA is detected into a control signal which is sent back to the VCA to control its gain. This technique can also be used in the digital domain, but because of the increased accuracy of digital processing over analog, we can also detect the signal prior to the gain changing element (a simple multiply in DSP), and send the appropriate control signal forward to the multiply instead. In this case, for a compressor, we will need to create a multiply coefficient that decreases as the input signal increases. As an example, for a constant output level of say, 1.0, a signal of 0.1 magnitude would need a multiplication coefficient of 10, whereas an input signal of 0.5 would require a multiplication coefficient of 2. The 1/X function implies a divide (the number 1 divided by our signal level, X); although multiplication is direct and simple with binary circuitry, division is not. To perform the required 1/X function, LOG and EXP can be used again, as 1/X = EXP(LOG(1)-LOG(X)). The FV-1 supports both LOG and EXP for this purpose (and many others), but be aware: Due to fixed point math, these functions require careful thought and planning in use.
Expansion is a handy tool, often simply for noise reduction; if a threshold level can be established, below which the signal is not useful, then a detector and multiply arrangement can be configured to gracefully decrease the signal path gain when the input signal level is below that threshold. The effect of a raging, distorted instrument jumping out of a perfectly silent background can be stunning.
As an effect, one processor input channel could be used to control another channel's gain; an instrument could be 'gated' by the signal amplitude from a different source, giving the impression of extreme 'tightness' to a performance.
Distortion
Finally, distortion is not an effect that digital systems handle gracefully. Since the samples that are being mathematically manipulated only represent a signal bandwidth up to half the sample rate, any non-linear effect (such as distortion) will produce higher harmonics; if these harmonics ever represent frequencies beyond the Fs/2 limit, they will 'fold' down to the DC to Fs/2 frequency range, where the result will no longer be in harmonic relationship with the original signal. Details of this alias process can be found here. The sound is quite ugly. Although oversampled processing can be used with filtering (The execution of a process many times over within a program), oversampling techniques cannot fully remove the aliased components from a poorly thought through distortion process. It may be best to generate distortion with math functions that are deliberately structured to create only low ordered harmonics that do not threaten to pass the Fs/2 threshold. This can be accomplished by the use of the 1/X function again (LOG, EXP). Allowing a signal to actually clip the number system extremes within the processor will certainly generate unacceptable harmonics and ugly alias tones, but this may be what you're looking for.
A second harmonic can be derived from an input sine wave by simply squaring the signal, (multiplying the signal times itself). If the signal is fairly well band limited, the output will be twice the input frequency, plus a DC offset equal to the peak amplitude of the input signal, that can be removed through various techniques. Unfortunately, the squaring technique causes the output amplitude to quadruple as the input amplitude is doubled, which may be too unnatural for the desired effect. Alternatively, a technique that 'rounds' off the tops of signals can be used to generate limited harmonic content, and warm intermodulation distortion.
This technique essentially transforms the input X to the output Y (ignoring sign):
If X<1 then Y=X
If X>1 then Y=2 - 1/X
This allows the input to remain undistorted until it peaks at a value of 1.0; beyond this, the maximum amplitude that is possible at the output is +/-2.0, and would require an infinite signal amplitude to achieve this. Of course, the actual signal levels will not be greater than +/- 1.0 in the FV-1, at the input or the output, so signal scaling will be necessary to perform this non-linearity. The sound however, especially for a guitar and keyboard instruments, is very nice, and aliasing is largely avoided. This concept delivers nice distortion, that is, lower level signals are clean, and only 'break up' on transients and emphasized instrumental notes. Distortion can of course be generated by other non-linear means, but alias will become an increasing problem.
Delay effects
The first popularized use of flanging was highlighted in the song 'Itchycoo Park' by Small Faces, recorded 40 years ago. Flanging is one of the fun things that can be done with a pair of analog tape recorders, which today may be difficult to find. In the days of analog tape, two recorders were set up with identical tapes, the outputs mixed together, and played at the same time. If one recorder was slowed slightly, so that the two would be slightly out of synchronization, a remarkable effect would emerge. As the opposite recorder is slowed, the two machines would cross through synchronization again, and when the sound passed through synchronization, the effect would seem to go 'over the top', an ecstatic, even orgasmic audio experience. The term flanging comes from the method of slowing a given machine, by lightly touching the flange of the source reel of a recorder to slow it down a bit.
When an audio signal is mixed with a delayed version of the same signal, the frequency response of the mixture takes on a very interesting shape. Such an arrangement is called a 'comb filter', on account of the frequency response shape:
The plot is from 0 to 20KHz, on a linear scale. We can imagine that two sine waves, one shifted in time from the other will reinforce or cancel, depending on the frequency and the delay. In the case of the 1mS delay shown above, a 1KHz signal will be exactly in phase with the same signal delayed by 1ms. 500hz though, will be shifted by the delay by exactly 1/2 cycle, and the delay input and output will cancel when mixed together. The plot shows peaks at 0Hz, 1KHz, 2KHz and so forth, and dips at 500Hz, 1.5Khz, 2.5KHz and so on. When music is played through such a filter, and the delay is varied, the peaks and dips of the frequency response move throughout the audio spectrum creating the 'flanging' sound. Notice that if the phase of one of the signals is inverted (multiply by -1.0) at the mixer, the exact inverse of the frequency response is obtained, peak frequencies being converted to dips, and vice-versa.
This flanging effect can be psycho acoustically explained. Our ears are roughly 6" apart, and since the speed of sound is roughly 1000 feet per second, a sound to the right side of our head will arrive at the right ear about 0.5mS prior to arriving at the left ear. Our brains can determine the location of a sound source based on this delay time. In fact, signals are traditionally panned in stereo space by the adjustment of the relative sound level in the two stereo channels, but if a mono signal is fed directly to one stereo channel, and through a 0.5mS delay to the other, the level will be the same in both channels, but the listener (with headphones) will clearly identify the sound as coming from the 'early' side. This psycho acoustic panning can be used as an interesting effect. Flanging, with a continuously varying relationship between the early and late sounds, gives the effect of one's head slowly turning in space, as though the listener was floating and turning before the sound source. Interestingly, this is also the case even when the flanged sound is auditioned in mono.
Flanging programs usually sound best when the delay modulation is linear with time, that is, the delay changes by some constant fraction of a sample on every sample cycle. Often this is accomplished by setting up a software Low Frequency Oscillator (LFO) to produce a triangle waveform, with the peak of the waveform representing zero delay (over-the-top). Further, some feedback can be applied around the entire flange process to accentuate the effect. All variations on the theme are fair game: negative summation, as well as negative feedback around the flange block, even a higher frequency sine wave added to the LFO ramp!
In a DSP system with a sample rate (Fs) of 40KHz, 40 memory locations would be required to provide a 1mS delay.
As a note, when listening to a CD, the 44.1KHz sample stream is of course smoothed into a continuous waveform by the DAC in the system, but if one were to imagine the time period between samples and the speed of sound, the physical space between samples as the sound emerges from a speaker would be a little more than 1/4 of an inch per sample.
The Hass effect
When listening to two identical sounds mixed together, one delayed from the other, the sound quality is affected as a tone when the delay is short, and two distinct sounds if the delay is long. The delay time that lies between these two extremes is about 30mS, and the overall idea is called the Hass effect. Flanging is usually accomplished with rather short delays, causing the lowest primary notches to be around 100Hz (5mS delay). Longer delays verge on the impression of two sound sources, so the effect of chorus and vocal doubling both require delays at or around the magic 30mS range.
Chorus and Vocal doubling
The simplest method of 'fattening' an instrument or voice in the studio is to add extra tracks of a similar performance, as though an entire ensemble of musicians were performing at once. In actual performance, this may be impossible, so the effect of chorus can be used instead. Chorus is usually a delay, or multiple delays, all on the order of 20mS to 50mS long, slowly modulated by LFOs to produce slight variations in both pitch and time throughout the performance. Too fast a delay modulation can lead to vibrato effects, a subject which can be jumped to from here.
Vocal doubling, also referred to as slap-back echo, refers to a short delay that is used to fatten a voice, usually without much or even any delay modulation. Vocal doubling delays can be in the 30ms to 60mS range.
Phase shifting
The effect of frequency response notches moving in time, produces the head-turning-in-space effect, but may not need a true variable delay to be accomplished. The effect of phasing can be created by producing a few notches in the audio spectrum, and modulating their frequency slowly with time, to produce a similar effect. In analog electronics, this is done with a bank of all-pass filters, circuit elements that have a flat frequency response, but create a frequency dependent phase shift. The output of the filter bank is summed with the input, and at those frequencies where the filter bank output is out of phase with the input, a notch is created.
The all pass filter operation is complicated to explain, but the analog and digital versions are shown here:
In both cases, the output is in phase with the input at low frequencies, but out of phase at high frequencies. Varying the resistor value in the analog version, or the K value in the digital one, will adjust the frequency where the phase is at the midpoint, 90 degrees. This filter is useful in not only making phase shift effects, but others as well. In the case of the digital variant, the delay is a single memory location (a register), but we will see later in the section on reverb where the digital all pass filter can make use of a longer internal delay.
Notice that the phase shifting effect produces only a few, lower frequency notches, whereas the flanger, using a real variable delay, produces notches out to the highest frequencies. Psycho acoustically, the lower frequency notches are responsible for the majority of the effect. In fact, when building digital flangers, you may wish to use a filter to slightly roll off the upper frequencies from the variable delay signal; the large number of notches at the highest frequencies can often become a 'distraction' to the intended effect.
A Note on the FV-1 Delay memory addressing
In a general purpose processor, memory is accessible as a block with fixed addresses. If you wish to implement a delay, you must write to a new location on every sample cycle, then read from a different location that is also changing on every sample cycle, ultimately reading the originally written data some number of sample cycles later. On each memory access, you must somehow calculate the memory address for each operation, for both reading and writing. The FV-1 is designed to do this for you, automatically. All accesses to the delay memory (but not the register bank) are to addresses that are automatically generated from a relative address that you specify in your program, plus a memory offset counter that decrements at the start of each new sample cycle. As a result you can write programs that initially define the areas of memory you wish to use for delays, and in your written instructions you can refer to the start, end, or any point between the start and end of a delay when reading signal outputs. Writing is usually to the start of the delay, the base address.
When using this scheme, you must be aware of it, but you can largely ignore concerns for all of that which is going on in the background.
Continuously varying delays
When we attempt to change a delay in a DSP program, we can hardly jump from one delay length to another, as this would cause abrupt changes in the sound. Normally, we would establish an area in memory for the maximum delay, and change the delay length by adjusting the read point from memory. When smoothly varying a delay, the specific delay point we calculate will often lie between two delay samples. The easiest way to obtain such a fractional delay output result is through linear interpolation between the two adjacent samples. We read each of the two samples and multiply each by it own interpolation coefficient, then sum these two products to obtain a valid mid-sample result. The interpolation coefficients must both sum to unity. In practice, a virtual address is calculated in the DSP code, which is then used to access a read point form memory.
An example:
Notice that the closer the virtual sample is to a real one, the higher the interpolation coefficient. Confusing the proper interpolation coefficients is a common mistake in writing DSP programs.
Vibrato
Vibrato is technically a repetitive variation in pitch at a frequency that usually lies in the range of 2 to 6 Hz, and is different from tremolo. This is accomplished by a short variable delay, the delay time being modulated by a sine wave. As the delay shortens, the pitch of the output will raise, and as the delay lengthens, the pitch will fall. Attempting to obtain a constant pitch change from this technique will quickly lead to running out of memory, but if the delay is modulated with a sine wave, vibrato can be accomplished with a small delay. The pitch change is the result of the rate of change of delay. If you code a vibrato using say, a 2mS delay, and modulate it over its entire range with a sine wave LFO, the pitch change will be three times as great at 6 Hz than it will at 2 Hz.
The extremes of the pitch change can be calculated, using some simple logic: The LFO will be producing a sine wave that in the above case will modulate a 1mS delay by a +1mS and a -1mS amount, leading to a delay that spans 0 to 2mS. Sine waves have the property that at their greatest rate of change is while crossing zero, and at this point, the rate of change is 2*π *F*peak amplitude. At an LFO frequency of say, 4Hz, the sine wave will be changing at 2 * π * F * the peak delay variation, or approximately 2*3.1415*4*1mS=25.13mS/second. This is to say that the pitch will be changed by about 0.02513 of it's original value. In music, one semitone represents a frequency increment of about 0.059 (roughly 6%). This 4Hz, +/-1mS vibrato would produce a peak pitch variation of about 1/2 a semitone, which may sound extreme in some cases, but then, not enough in others.
Chorus effects will also demonstrate a vibrato effect, as any changing delay will affect pitch. This is often the limiting factor in the chorus effect, as too great a delay sweep will lead to extreme off-notes. Then again, this may be the objective.
Pitch transposition
Pitch transposition is a change in pitch that corresponds to music; that is, it is a change by a factor, not an increment. To illustrate, an octave is a factor of two in frequency. If you were to pitch transpose a 1KHz tone up an octave, it would become 2KHz, and if brought up another octave, 4KHz. Transposition of music allows the pitches to remain in musical harmony, simply set into a different key.
To perform pitch transposition, we will need to use variable delays, but as we already know, we cannot change a delay, increasing or decreasing its length for very long, or we will eventually run out of memory. To retain the basic character of the music while changing its pitch through a variable delay technique, we will need to occasionally change our moving delay read pointer as it approaches one end of the delay to the opposite end of the delay, and continue on. This abrupt jump in the read pointer's position will be to a very different part of the music program, and will certainly cause an abrupt sound. The problem can be largely overcome by establishing two delays, let's name them A and B, both with moving read pointers, but with their pointers positioned such that when the read pointer of delay A is just about to run out of 'room', delay B's pointer is comfortably in the middle of it's delay's range. We then cause a crossfade, from obtaining our transposer output from delay A to the signal coming from delay B. When the delay B pointer begins to run out of space, (just prior to pointer repositioning), we crossfade back to delay A. The delays can in fact be a single delay, with two read pointers properly positioned.
The rate at which we crossfade, the delay lengths we use, and the amount of pitch transposition we require will determine the resulting naturalness or unnaturalness of the transposed result. In many cases, especially for complex music, the effect is quite believable.
Barber pole flange
A fractional pitch transpose, a detuning of only perhaps a tenth of a percent, when added with the input, can cause an effect called 'barber pole flanging'. Like the rotating red and white spiral that would be outside barbershops as an advertisement, This flanging sound seems to always be sweeping up or down, continuously. It is a very interesting and useful effect. For best results, this is done with a very short delay, and the signal to which the result is added should be delayed a bit too. Experimentation is necessary.
Pitch shifting
Pitch shifting is different from transposition. While transposition is a change in pitch by a factor, pitch shifting is by an increment. The two terms are often confused, and used interchangeably to describe the more common and useful pitch transposition. If we pitch shift by 1KHz, then 1KHz becomes 2KHz, and 2KHz becomes 3KHz; not a pleasant musical transformation! Pitch shifters are used to disguise voices and create non-harmonic effects, and when used in conjunction with transposers can allow a talk show host to have hilarious conversations with himself (as with Phil Hendrie (sorry Phil)).
The pitch shifting process makes use of the interesting mathematical properties of sine waves, and their 90 degree phase shifted brothers, cosine waves. The process effectively multiplies an LFO by the input signal, but must do so using complex math. By complex is meant not just difficult and complicated, but instead, the use of SIN and COS LFO signals, and the use of both the input signal and a copy of the input that is shifted 90 degrees in phase.
Obtaining an input signal copy that is phase shifted by 90 degrees would be easy if just a single input frequency was involved, as we have already seen the rather simple all-pass filter that will perform this function. To produce a constant 90 degree phase shift over a wide frequency band however, is a bit more difficult.
The terms SIN and COS are from an LFO that produces these two signals, and the amount of pitch shift will be the frequency of the LFO, in Hz. The input phase shifter is actually two banks of all pass filters that are designed to produce a continuously varying phase with frequency, and the difference between their outputs is approximately 90 degrees over a wide frequency band. In practice, the input to the COS multiply is from one phase shifter, the input to the SIN multiply is from the other. Take note that any input DC value (input offset) will be also shifted, causing the LFO frequency to be found at the output! The pitch shifter will pitch shift either up or down, based on the phase relationship between SIN and COS; normally, SIN lags COS by 90 degrees, but if your LFO can be driven to produce a negative frequency (as in the FV-1), then COS will lag SIN. Pitching up and down then becomes a matter of the LFO producing a positive or negative frequency. Wild notions, no?
Designing the all pass filter banks for the pitch shifter is difficult; a task made easier by limiting the signal frequency range to only that which is required. For voice, perhaps 100Hz to 6KHz will do.
Tremolo
Where vibrato is the sinusoidal variation in pitch, tremolo is the sinusoidal variation in amplitude. This is easily accomplished by simply multiplying the input signal times an LFO sine wave that varies from 0 to 1 (instead of -1 to +1). Because the average signal level will result in being half of the original, you may consider multiplying the input by a 0 to 2.0 sine wave, or simply adding gain to the algorithm.
Ring modulation
This is simply tremolo at a higher rate, and with the LFO swinging both + and -. An ugly sound, which might be exactly what you're looking for. This is perhaps the the most repulsive of the ugly sounds, so if that's you're interest, it is the most beautiful of the ugly sounds.
Simple filters
Filters can come in all shapes sizes, types and styles, simple or highly convoluted, easy to come up with coefficients for, or agonizingly difficult. The subject is huge, and applications are vast. The simplest filter is the single pole low pass:
The cutoff frequency is determined by K1 and K2, the sum of which must be equal to 1 for the filter to have unity gain. For a given sample period t and a desired -3dB cutoff frequency of F, the value for K1 is equal to e-(2πFt) . This illustration shows the filter being accomplished with two multiplies, but since K1+K2=1.0, it can be done with one multiply thusly:
The single controlling coefficient, K2, adjusts the -3dB point, and is equal to 1-K1 in the previous equation.
A high pass filter can be constructed from the low pass, by simply subtracting the output from the input of the low pass design, and shelving can be provided by an adjustable coefficient. The shelf coefficient Ks should be negative to perform the subtraction, and would be set to -1.0 for the shelf to be infinite.
Because they are so useful, especially in reverb algorithms, special instructions in the FV-1 can perform this shelving high pass filter in two successive instructions.
The shelving low pass can be a derivative of the high pass with an infinite shelf:
The FV-1 can also produce this structure in two successive instruction cycles.
One characteristic of the single pole filters is that the cutoff frequency is linearly dependent on the coefficients when used at the lower operation frequencies. Therefore, although the single pole characteristic is not dramatic as an effect, the frequency can be swept with simple mathematical functions from control signals such as a potentiometer position or a detected signal level. For the lower, more musical frequencies, K2 is roughly equal to (2πF)/Fs, where F is the cut off point, and Fs is the sample frequency.
Audio effects DSP applications are distinctly different from precision instrumentation DSP systems. The former only requires the desired resulting sound, which in most cases has no need for precision and leads to simple hardware; the latter however, may require high accuracy and precisely derived coefficients. Music is to one's taste, which is imprecise by nature! Programming an effects DSP is more of an art, programming a scientific instrument is solidly in the realm of mathematics. This gives the effects programmer a significant degree of freedom in choosing DSP structures that may not be perfect, but accomplish the task quickly and with easily derived coefficient values.
Peaking filters
Bandpass filters and peaking low pass or high pass filters require a 2-pole design, which is considerably more complicated. There are several approaches, but the most straightforward is the biquad filter. This filter uses two integrators in a loop, and can produce high-pass, low-pass, band-pass and notch outputs, depending on how signals are input, and how outputs are taken. An integrator is simply a register and an adder, connected so that the register contains the continuous summation of input samples. Two integrators in a loop (with a sign inversion of the signal at one point) will form an oscillator, the frequency depending on the coupling coefficients. An oscillator is simply a peaking (bandpass) filter with infinite Q and a stimulated starting condition:
This is the structure of the SIN/COS LFO element in the FV-1, and when coded into a program can be the starting point for musical peaking filters. Signals could be introduced anywhere within the filter, but since an infinite Q filter will have infinite gain, it is of little practical use (although you may find that application!). The Kf value is used twice, and would be calculated (for low frequencies) much the same as K2 in the earlier, single pole filters. To become a more useful filter, the Q must be lowered (by introducing losses), and signals must be input and output. Filters of this type are very useful at lower frequencies, but are limited to peaking frequencies below about Fs/4. For most music applications, sweeping through the fundamental and lower harmonics of a signal, this is entirely adequate.
With a Kq value of perhaps -1.0, this filter is also a great way to split a signal into high and low frequency bands, each with 12dB per octave slopes. Diminishing the value of Kq will increase the filter's Q. In a sense, we may better consider Kq to be a damping coefficient. The filter produces a high pass output (HP) that is symmetrical with the low pass output (LP), and a band pass peak as well (BP). A notch can be created by adding HP and LP together. This is a remarkably flexible filter and easy to code. The above structure is particularly useful as a swept filter, as the filter's frequency is controlled entirely by Kf, in a linear fashion. The Q of this filter will remain reasonably constant over a wide range of Kf values.
If peaking (or cutoff) frequencies higher than about Fs/4 are required, they will be difficult to do without oversampling the filter. Oversampling simply means that the algorithm is written twice within the program, so to have the effect of being executed twice as often on the data samples. This technique allows the above filter to be swept over the entire DC to Fs/2 bandwidth.
In the case of fixed filters, ones that are not meant to be swept, a different architecture can be used, but as the coefficients are interdependent, changes to the coefficients cannot be done casually. The advantage of fixed filters is that they can reach to Fs/2 without the use of oversampling techniques. An example of one basic structure:
This filter form requires coefficients that must be calculated from an analog filter that has the required response, and such coefficients cannot be experimentally derived or modified with ease.
Reverberation
Echo can be easily achieved with a long, recirculating delay:
This is the typical 'karaoke sound' that was popularized in the 70's due to the development of analog delays using charge-coupled IC techniques. The tradition continues with karaoke today, despite the availability of the more desirable digital reverberation. The echo effect is in fact just a low reverberation density approach, but can still be characterized in terms of reverb time by measuring the time for a recycled impulse to fall by 60dB.
A more realistic abstraction of a natural reverberant space is produced by more complicated processing structures. The primary difference between echo and reverberation is a dramatic increase in reverb density, both initially, and with time as the reverb 'tails out'. This increase in density is provided by the all-pass filter, similar to the one used in phasing, but with a multi sample delay used in place of a single register. The all pass filter uses identical coefficients, but of opposite sign. The signs of the coefficients can be swapped (for reverb applications), causing a similar sound, but a different impulse response:
The important characteristic of the allpass filter, when built around a sizable delay is that although the impulse response is made more complicated, which is desirable in a reverb system, the frequency response, measured over a period of time, is flat. Recalling from the earlier discussion about delays, the summation of a delay with it's input causes a comb filter response, which far from flat. The FV-1 has the ability to perform the mathematics of an allpass filter stage (with fixed coefficients) in two successive processor operations.
When multiple delays and all pass filters are placed into a loop, sound injected into the loop will recirculate, and the density of any impulse will increase as the signal passes successively through the allpass filters. The result, after a short period of time, will be a wash of sound, completely diffused as a natural reverb tail. The reverb can usually have a mono input (as from a single source), but benefits from a stereo output which gives the listener a more full, surrounding reverberant image. A simple reverb loop:
The terms Lsum and Rsum are taps from the delays, meant to be added (not shown) in different proportions to produce a stereo-like output. The coefficients are shown within the circles for simplicity. The term Krt controls reverb time. Shelving high pass and low pass filters may be added to the loop to control the decay of high and low frequencies, which produces a more natural reverberation, but are not shown. This loop is composed of four blocks of 2 allpass filters and a delay, although any of the blocks could contain 1 or 3 or more allpass filters, and the loop could be 2 or 3 blocks instead. There may be only one Rsum or Lsum per delay, and the input may be inserted at only 2, or even 1 spot within the loop. Stereo may be input by inserting the left input to one point in the loop, and the right input to another. Further, it is often useful to add a few series allpass filters in the input signal path, so that the signal inserted into the loop has a higher initial density. The construction of a reverberator architecture and the choices of filters, delays and output taps is very much an experimental art; there is no 'best' algorithm, just as there are no 'best' rooms, halls, or plates in the physical world.
Reverberators can be built that sound wonderful with drums; explosive, smooth and rich in a wash of density, and when coded in the FV-1, can be accomplished with as few as 20 instructions. When auditioned with a single sound however, they may have a 'ringing' tail sound, at the very end of the reverberation time. Many commercial tracks are cut with such ambience, but inexperienced engineers will be concerned about the ringing tail sound. In fact, this is entirely covered up by the active music in actual use. To remove the ringing sound, it is helpful to slowly modulate some of the delay lengths within the reverb loop, so that the output pattern is not fixed, but slowly varying, which smoothes out repetitive mechanical effects. This can be accomplished by a single SIN/COS LFO generator, modulating the lengths of one or two of the internal delays (delays or all-pass delays), using say, the SIN output in one place and COS in another.
The initial sound of a reverberator can be an important part of its overall quality, and is often achieved by the use of a tapped delay:
There can be any number of taps, each weighted by a multiply coefficient that exponentially decays with delay time. These initial reflections give a sense of dimension to the reverberator. The left and right outputs can be from different taps, giving a sense of direction to the 'room'. The left and right taps are summed with the taps from the reverberator which produces the reverb 'tail'.
Considerations when building a reverb
Do not expect a given reverb structure, with delays and coefficients well chosen, to sound good at extremes of reverb time. To build a good reverb is one thing, to build one that responds well over a wide range of decay times is extremely difficult; impossible, if not extremely complicated in design.
The total delay (excluding allpass filter delays) in the loop should be at least 200ms. Shorter delay time will lead to flutter, a repeating quality in the tail. The human ear is very sensitive to flutter in the 4 to 8 Hz range; very short delays will cause a tinny sound, moderately short delays will cause a noticeable flutter. If the flutter frequency is low, on the order of 1 to 2 Hz, the ear perceives the sound as 'evolving', not fluttering.
Placing variable delays in the allpass filters, even just in one spot or another, can help smooth out a reverb, giving the slight impression of motion, and suppressing a hardness, ringing or flutter problem.
The swapping of coefficient sign in some of the allpass filters can occasionally improve the overall quality.
Allpass filters with a coefficient of 0.5 will cause the reverberator output to 'build', leaving the listener with the impression that there is a delay in the reverb output; this can be improved with some early reflections from a tapped delay. Allpass coefficients on the order of 0.6 will build quicker, but be 'fat' during the initial sound period. Coefficients of 0.7 and above will sound more immediate, but can have the tendency to produce a 'ringing' sound.
Feeding the input into each block of the loop, and taking outputs, both left and right from each delay will lead to a very dense reverb, but because of the comb filter effects that are then produced, the reverb will not have a flat frequency response characteristic. Complete flatness of response is not really required, but sharp and narrow peaks of high amplitude cause the reverb to 'ring'. Consider taking fewer taps as outputs and inject the signal less often to get a flatter response.
Gated reverb and dynamic effects
Any signal can be detected and filtered, and in doing so, turned into a control parameter. In the case of reverb, the input signal can be detected and used to control reverb time. While the signal is active, above a certain threshold, the reverb time could be long or short, and then smoothly (important!) transform to the opposite extreme when the signal goes away. This can produce a powerful effect on drums, where the reverb is huge for a brief time, and then rather suddenly extinguishes some short time after the signal has gone. Likewise, a singer's voice can be surrounded with a fairly short reverb time while singing, which may lead to greater clarity, but then extend to a longer time between phrases.
Dynamic effects can take on any number of dimensions; truly an art form of high complexity. Peaking filters that track a signal's level ('autowah' effects) are a classic, but not a limiting example. LFOs that drive phasers, flangers, vibrato or pitch effects can be modulated in both value, amplitude, rate or intensity, depending on the effect and the desired results.
Signal detection is performed by several means: We could convert the normally +/- swing of the signal into + only, and then average the result with a low pass filter (average detection). We could alternatively use the more musically relevant RMS (root-mean-square) detection, which gives a result that is more closely related to apparent loudness; RMS detection requires that the signal be squared (multiplied by itself), which produces a positive output value, then averaged by a low pass filter, and finally square-rooted by the use of LOG and EXP functions, as the square root of (X)=EXP(LOG(X)/2). Finally, we could peak detect the signal into a filter, where any signal peaks that exceed the filter's value are loaded into the filter register. All of these techniques can find their way into controlling effect parameters.
When controlling the frequency of a filter, be aware that the musical scale is exponential, not linear. For example, if a filter frequency is to be controlled by a potentiometer, perhaps over the four octave range of 100 to 1600 Hz, the center of the pot would best represent 400 Hz, not 800Hz. The FV-1 contains both LOG and EXP functions so that such musically relevant conversions can be performed easily.
Compression and expansion
The control of program dynamics can be an important part of any effects toolkit. In the analog world, a VCA (voltage controlled amplifier) is often used to control gain, and in the case of a compressor (or limiter), the output of the VCA is detected into a control signal which is sent back to the VCA to control its gain. This technique can also be used in the digital domain, but because of the increased accuracy of digital processing over analog, we can also detect the signal prior to the gain changing element (a simple multiply in DSP), and send the appropriate control signal forward to the multiply instead. In this case, for a compressor, we will need to create a multiply coefficient that decreases as the input signal increases. As an example, for a constant output level of say, 1.0, a signal of 0.1 magnitude would need a multiplication coefficient of 10, whereas an input signal of 0.5 would require a multiplication coefficient of 2. The 1/X function implies a divide (the number 1 divided by our signal level, X); although multiplication is direct and simple with binary circuitry, division is not. To perform the required 1/X function, LOG and EXP can be used again, as 1/X = EXP(LOG(1)-LOG(X)). The FV-1 supports both LOG and EXP for this purpose (and many others), but be aware: Due to fixed point math, these functions require careful thought and planning in use.
Expansion is a handy tool, often simply for noise reduction; if a threshold level can be established, below which the signal is not useful, then a detector and multiply arrangement can be configured to gracefully decrease the signal path gain when the input signal level is below that threshold. The effect of a raging, distorted instrument jumping out of a perfectly silent background can be stunning.
As an effect, one processor input channel could be used to control another channel's gain; an instrument could be 'gated' by the signal amplitude from a different source, giving the impression of extreme 'tightness' to a performance.
Distortion
Finally, distortion is not an effect that digital systems handle gracefully. Since the samples that are being mathematically manipulated only represent a signal bandwidth up to half the sample rate, any non-linear effect (such as distortion) will produce higher harmonics; if these harmonics ever represent frequencies beyond the Fs/2 limit, they will 'fold' down to the DC to Fs/2 frequency range, where the result will no longer be in harmonic relationship with the original signal. Details of this alias process can be found here. The sound is quite ugly. Although oversampled processing can be used with filtering (The execution of a process many times over within a program), oversampling techniques cannot fully remove the aliased components from a poorly thought through distortion process. It may be best to generate distortion with math functions that are deliberately structured to create only low ordered harmonics that do not threaten to pass the Fs/2 threshold. This can be accomplished by the use of the 1/X function again (LOG, EXP). Allowing a signal to actually clip the number system extremes within the processor will certainly generate unacceptable harmonics and ugly alias tones, but this may be what you're looking for.
A second harmonic can be derived from an input sine wave by simply squaring the signal, (multiplying the signal times itself). If the signal is fairly well band limited, the output will be twice the input frequency, plus a DC offset equal to the peak amplitude of the input signal, that can be removed through various techniques. Unfortunately, the squaring technique causes the output amplitude to quadruple as the input amplitude is doubled, which may be too unnatural for the desired effect. Alternatively, a technique that 'rounds' off the tops of signals can be used to generate limited harmonic content, and warm intermodulation distortion.
This technique essentially transforms the input X to the output Y (ignoring sign):
If X<1 then Y=X
If X>1 then Y=2 - 1/X
This allows the input to remain undistorted until it peaks at a value of 1.0; beyond this, the maximum amplitude that is possible at the output is +/-2.0, and would require an infinite signal amplitude to achieve this. Of course, the actual signal levels will not be greater than +/- 1.0 in the FV-1, at the input or the output, so signal scaling will be necessary to perform this non-linearity. The sound however, especially for a guitar and keyboard instruments, is very nice, and aliasing is largely avoided. This concept delivers nice distortion, that is, lower level signals are clean, and only 'break up' on transients and emphasized instrumental notes. Distortion can of course be generated by other non-linear means, but alias will become an increasing problem.